クルマ用のDC12V→AC100Vインバータを分解してトランスを取り出したのですが、インダクタンスが不明なので調べたときの、調べ方のメモです。(おことわり:Wikipedia 等で調べながら自己流の理解で説明していますので、誤りがあるかもわかりません。何なりとご指摘下さい。そして事前に間違いをお詫びしておきます)

開放試験
二次側を開放し、一次側にLCメータを接続すると、一次巻線の自己インダクタンス\(L_1\)が測定できます。これを開放試験と言います。今回のトランスはプッシュプルコンバータで使われる二次巻線を2つ有するトランスなので、二次巻線a、二次巻線bの両方を測定してみました。その結果、以下の測定値を得ました。
| 一次巻線 (pin1-2間) の自己インダクタンス \(L_1\) | 5.45 mH |
| 二次巻線a (pin3-5間) の自己インダクタンス \(L_{2a}\) | 0.050 mH |
| 二次巻線b (pin4-6間) の自己インダクタンス \(L_{2b}\) | 0.050 mH |
プッシュプル用のトランスなので二次巻線が対称に作ってあるはずで、実際そうなっていそうです。以後、2つの二次巻線の特性は等しいとみなし、二次巻線の自己インダクタンスを\(L_2\)と表します。
さて、自己インダクタンスは巻数の二乗に比例することから、この測定結果を使って巻数比が推定できます。以下の式に当てはめて、
\[ n = \sqrt{\frac{L_1}{L_2}} = \sqrt{\frac{5.45}{0.050}} = 10.4 \]
となりました。12V→100Vのトランスなので、計算上は8.33となるはずなのですが、かなり大きいです。12Vのバッテリーを繋ぐと125Vが出てくる計算になります。確かに、矩形波インバータでAC100V、つまり振幅141Vのサイン波と等しい電圧を作るためには、矩形波の振幅を100Vより大きくする必要があるので、これくらいなのでしょうか。うーん12対100とは何のことやら……。
短絡試験
二次側を短絡し、一次側にLCメーターを接続すると、一次側と二次側の漏れインダクタンスの合計を、一次側から見たインダクタンス\(L_{short1}\)として測定できます。これを短絡試験と言います。今回は、二次側の2つの巻線の特性はほぼ等しいとみなし、片方だけを測ることにしました。短絡試験により以下の測定値を得ました。
| 二次巻線aを短絡し一次側から測った漏れインダクタンス \(L_{short1}\) | 0.03 mH |
| 一次巻線を短絡し二次側aから測った漏れインダクタンス \(L_{short2}\) | -0.002 mH |
マイナスの計測値がありますが、きっとほぼゼロということでしょう。ちなみに、測るたびに計測値が2~3%変動しているので、参考程度に見てください。さて、ここから結合係数\(k\)を計算します。Wikipedia によると、JIS では以下のようにして結合係数を決めるようですので、当てはめて、
\[ k = \sqrt{1-\frac{L_{short1}}{L_1}} = \sqrt{1-\frac{0.03}{5.45}} = 0.997\]
となりました。ほぼ密結合なトランスであることが分かりました。
恐るべし接触抵抗
最初、二次巻線をワニ口クリップで短絡して短絡試験を行ったら、「5.21 mH」が得られました。二次巻線を短絡した状態としてはあまりにも大きすぎるだろうと疑問でしたが、原因は、ワニ口クリップと端子の接触抵抗およびワニ口ケーブル自体の抵抗にありました。トランスの巻数比が 一次 : 二次=\(N:1\) であるとき、二次側のインピーダンスを一次側に換算すると\(N^2\)倍になることは電気機器学などでよく知られた事実です。この原理により、二次側を短絡するワニ口クリップの接触抵抗が巻数比の二乗=109倍に拡大されてしまっていたようです。その大きな抵抗のせいで、LCメーターの読みが実値から大きくずれてしまったのです。したがって、二次側をはんだ付けできちんと短絡して測る必要があります。

漏れインダクタンスと励磁インダクタンスを計算
2つの試験結果から、電気機器学的な変圧器の表現で重要となる「励磁インダクタンス」と「漏れインダクタンス」を求めることができます。
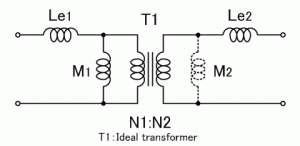
励磁インダクタンスは、自己インダクタンスのうち変圧器として機能する部分を表しており、上図に示す変圧器の等価回路で一次側に寄せて\(M_1\)、または二次側に寄せて\(M_2\)として表します。どちらに寄せるかは使用者の都合で決めますが、普通一次側に寄せることが多いです。今回は一次側に寄せて、
\[ M_1 = kL_1 = 5.43 \mathrm{mH} \]
を得ました。
次に漏れインダクタンスは、自己インダクタンスのうち変圧器として機能しないただのインダクタとなっている部分であり、上図の等価回路で一次側と二次側の両方に直列にくっつきます。下の式を用いて、
\[L_{e1} = (1-k)L_1 = 0.02 \mathrm{mH} , L_{e2} = (1-k)L_2 \approx 0.00 \mathrm{mH} \]
を得ることができました。
おわりに
トランスの等価回路には、電気機器学的な表現と回路理論的な表現があります。前者では「励磁インダクタンス」「漏れインダクタンス」を実用上重要なパラメータとして利用する一方、後者では「自己インダクタンス」「相互インダクタンス」「結合係数」をパラメータとしてトランスの性質を記述します。これら両方のモデルを行き来する方法が丁寧に解説された書物をあまり見かけない印象があるのは私だけでしょうか。電力×回路の花形であるパワエレ分野などで混乱が生じるような気もしてしまいます。